New blog post by Kate Stanton-Davies and Allan Lambert – April 9th 2024
Leakssuite Library is pleased to share a new blog post by Kate Stanton-Davies and Allan Lambert on UARL and CRLI – click here to read the full post
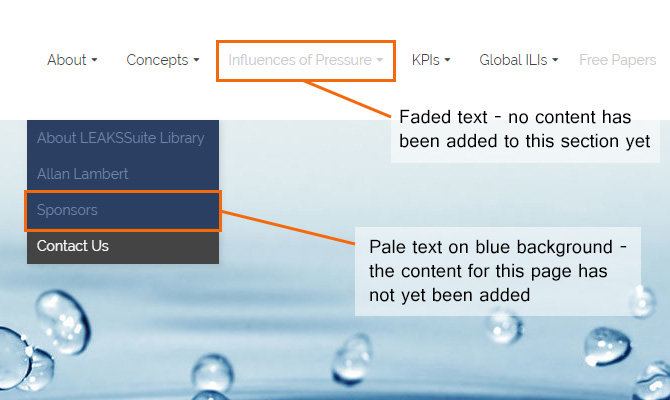
Menu Legend
You may have noticed that we’ve changed some of the link colours in the navigation menu. This is to indicate the pages which have now been updated from those on the previous Leakssuite website, and new pages added to LEAKSSuite Library.
Across the top level of links, a light grey colour means that no pages within this section have been updated yet.
Links with a dark blue colour in the dropdown menus indicate pages that haven’t yet had their content added.
World Water Loss Day
4th December 2020
Following 2 years research and development, LEAKSuite Library and Water Loss Research and Analysis Ltd are delighted to celebrate World Water Loss Day with Malta Water Services Corporation as the first Utility worldwide to receive customised UARL with SCF calculations for all 320 Zones and sub-Zones, allowing improved targeting of zones with potential for lower leakage.
Added November 2020
In the Concepts Section, the Economic ALC Intervention webpage was recreated in November, as a refreshed introductory webpage with links to two Keynote papers from 2005 which continue to be regularly referenced
Added June 2020
Two updated additions to the Concepts Section. IWA Water Balance and Random Uncertainty in Water Balance , both from the former LEAKSSuite website
Added August 2019
The Apparent Losses and IWS Sections became live in late August. These webpages provide site visitors with a link to a substantial source of free information on Apparent Losses, and on the activities of the IWA Intermittent Water Supply Specialist Group.
Added August 2019
The Apparent Losses and IWS Sections became live in late August. These webpages provide site visitors with a link to a substantial source of free information on Apparent Losses, and on the activities of the IWA Intermittent Water Supply Specialist Group.